Linear Combination and Span- Theoretical Definitions

In general terms, the simple definition of a linear combination is a multiplication of a scalar to a variable and addition of those terms.

For example:

If
$x$, $y$ and $z$ are variables,

and $a_1$, $a_2$ and $a_3$ are scalars,

the following equations will be a linear combination:

$v=a_1x+a_2y+a_3z$

Equation 6

Let's now put it into the Linear Algebra context.

Our variables will now be vectors: $\vec{x}$, $\vec{y}$ and $\vec{z}$ are variables.

The scalars can remain the same:
$a_1$, $a_2$ and $a_3$.

A linear combination of a scalar by a vector will be a new vector:

$\vec{v}=a_1\vec{x}+a_2\vec{y}+a_3\vec{z}$

Equation 7

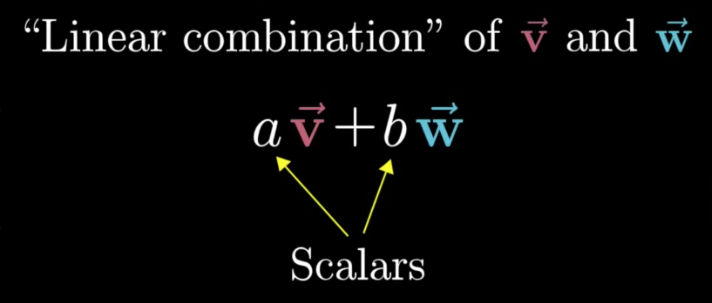
A linear combination can be of a single addition, or (as shown in equations 4 above) of any number of additions.

The general notation of a vector by a scalar linear combination will be:

$\sum_{1}^{n}a_i\vec{v_i}$

Equation 8

What is the Span?

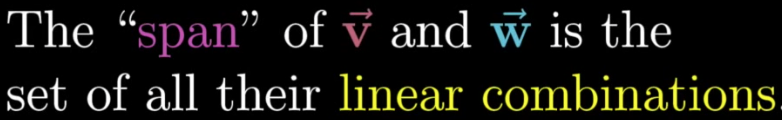
If $\vec{v_1}, \vec{v_2},….., \vec{v_n}\in \mathbb{R}$
then

the Span of those vectors (sometimes also referred to as the Linear Span) is the set of all possible linear combinations of those vectors.

Mathematically, the span of the set of vectors $\vec{v_1}, \vec{v_2},….., \vec{v_n}$ is written as:

$Sp(\vec{v_1}, \vec{v_2},….., \vec{v_n})$

For example:

The three following vectors: $\vec{v_1}=\begin{bmatrix} 1\\0\\0\end{bmatrix}$ , $\vec{v_2}=\begin{bmatrix} 0\\1\\0\end{bmatrix}$ and $\vec{v_3}=\begin{bmatrix} 0\\0\\1\end{bmatrix}$ span any vector in $\mathbb{R}^3$

To prove that, we will take a random vector $\vec{v}=\begin{bmatrix} p\\q\\t\end{bmatrix}$ and show that it can be generated as a linear combination of of vectors $\vec{v_1}, \vec{v_2}$ and $\vec{v_3}$.

In a quick observation we can see that:

$\vec{v}= p\begin{bmatrix} 1\\0\\0\end{bmatrix}+q\begin{bmatrix} 0\\1\\0\end{bmatrix}+t\begin{bmatrix} 0\\0\\1\end{bmatrix}$